Class 12 NEB Math Question 2079
Check this: NEB Class 12 Math Model Question Paper 2079 With Solution
The NEB Class 12 Math syllabus covers a variety of topics, including algebra, geometry, trigonometry, and calculus.
Welcome to our collection of NEB Class 12 Board exam questions 2079!
Today, we are sharing two set of questions from previous board exams, based on the latest NEB syllabus for 2079. These questions come with complete solutions to help you understand the material better. In the future, we will be adding more questions from different provinces as we receive them. If you have any questions about any subject, please feel free to email us at yt.narayannepal@gmail.com .
You can find the questions and answers in PDF form, which you can download from the end.
SET 1:
Sub Code: 0081 ‘K’
NEB-Grade XII
2079 (2022)
MATHEMATICS
New Course
For regular students (excluding technical stream’s students)
Candidates are required to give their answer in their own words as far as practicable. The figures in the margin indicate full marks.
Time: 3 hrs.
Full Marks: 75
Attempt all the questions.
Group ‘A’
Solution of NEB Class 12 Math Question Paper 2079:
To access the NEB Class 12 Math Question Paper 2079 with solutions, simply click on the ‘Download Now’ button and wait for 10 seconds for the PDF to be downloaded.
These questions and solutions have been provided by NARAYANNEPAL to help students prepare for their exams. Make sure to utilize these resources to increase your chances of success on the NEB Class 12 Math exam.
Download Both Question & Answer
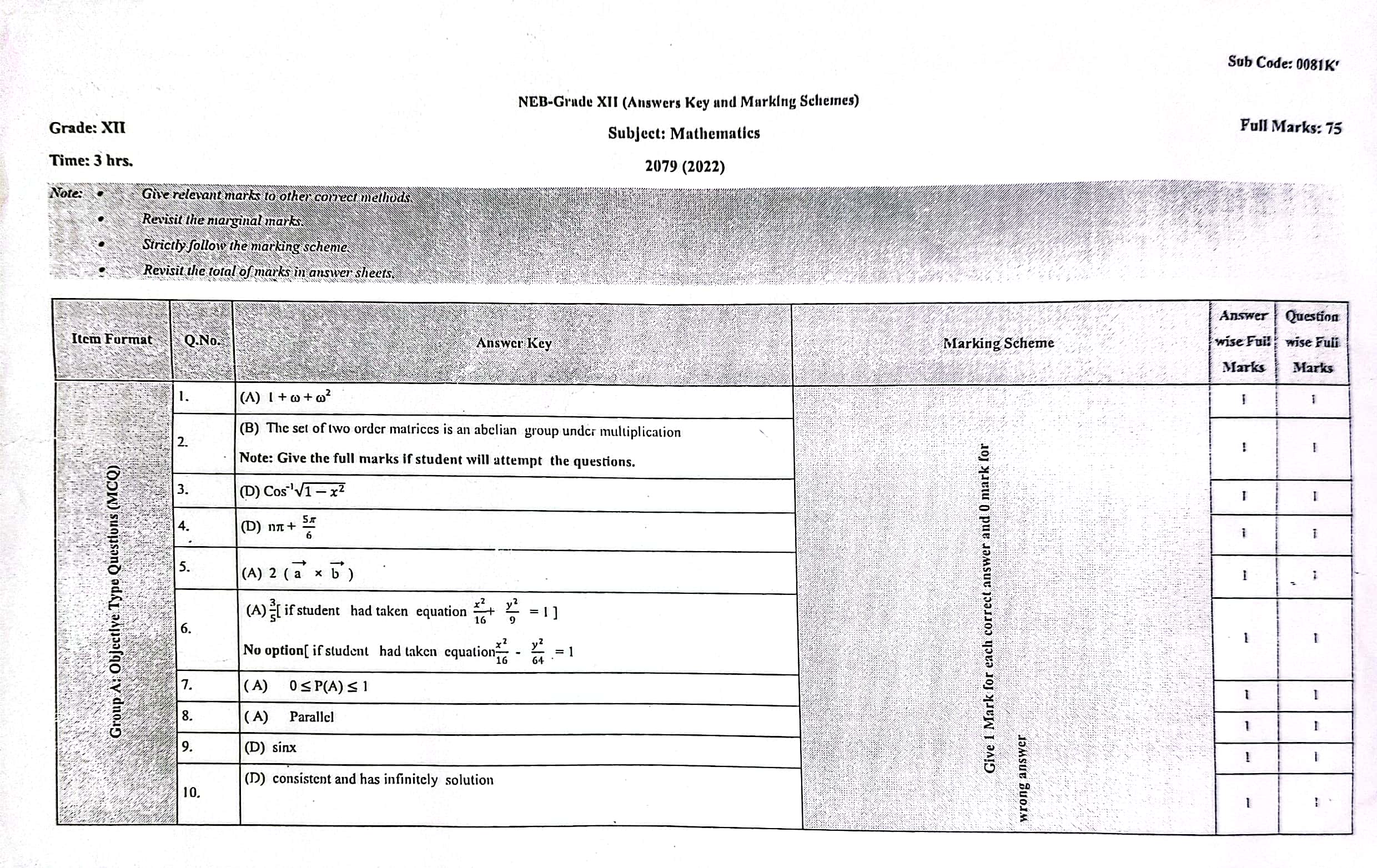
SET 2:
Sub Code: 0081 ‘J’
NEB-Grade XII
2079 (2022)
MATHEMATICS
New Course
For regular students (excluding technical stream’s students)
Candidates are required to give their answer in their own words as far as practicable. The figures in the margin indicate full marks.
Time: 3 hrs.
Full Marks: 75
Attempt all the questions.
Group ‘A’
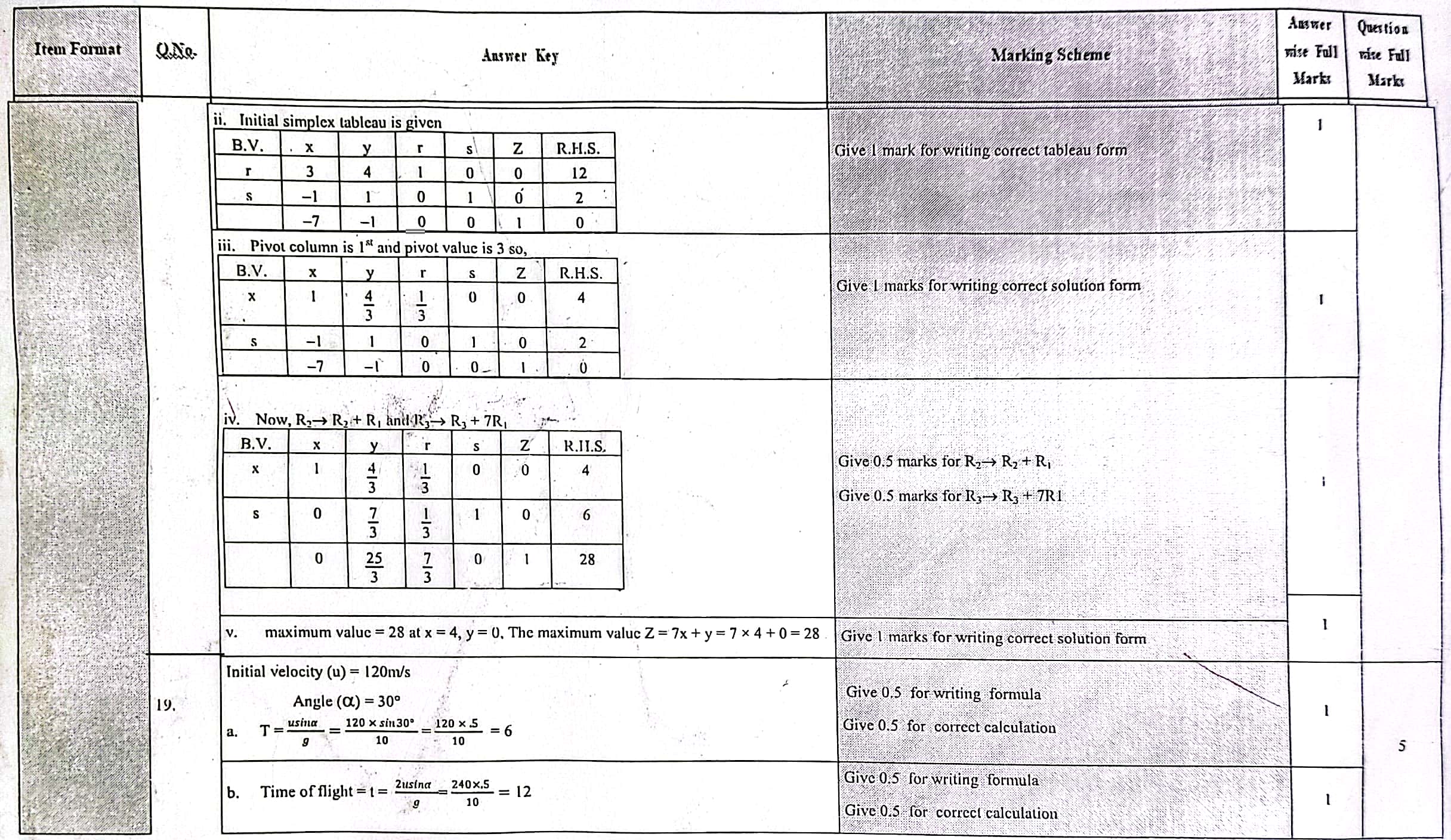
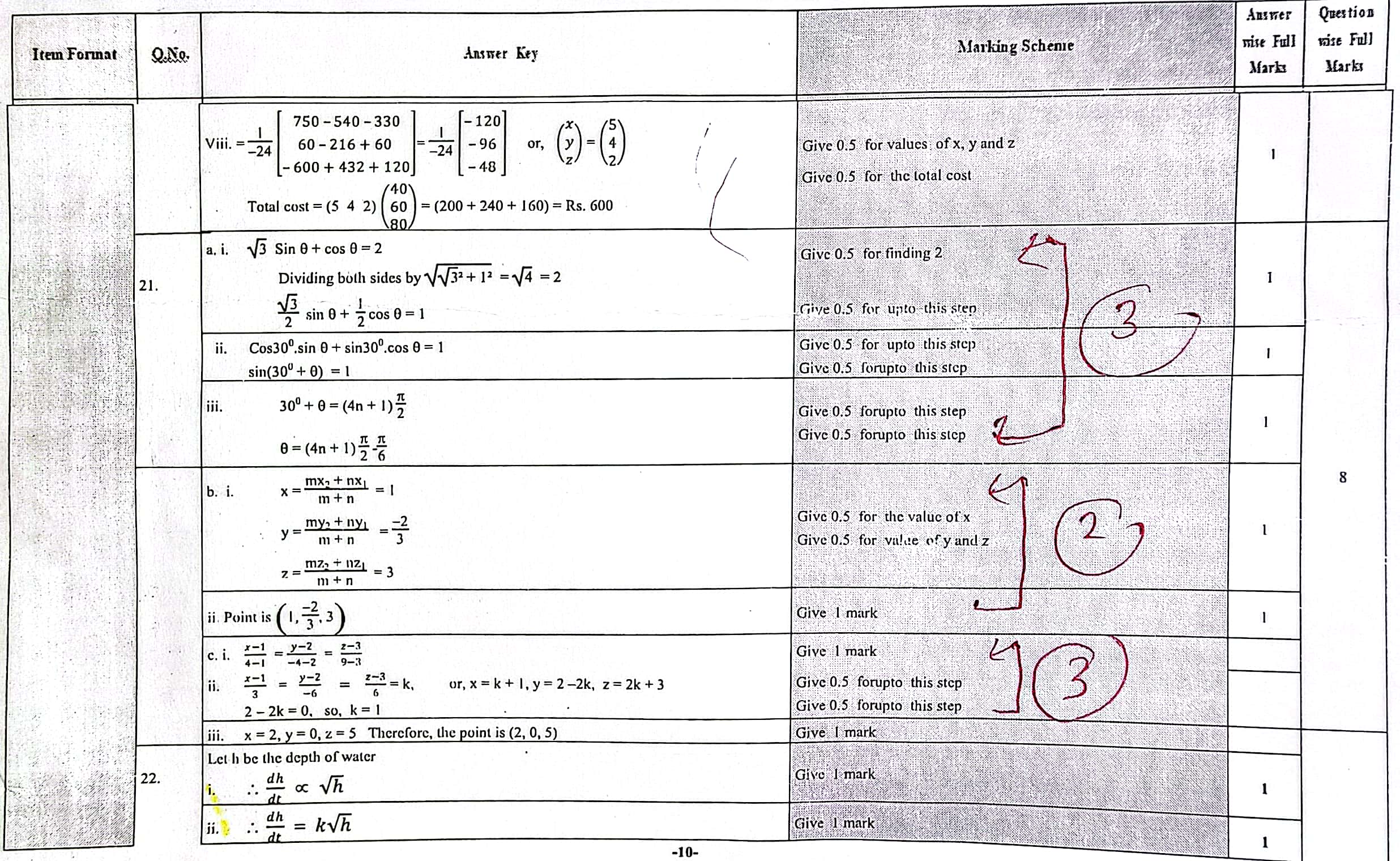
Solution of 2nd Set of NEB Class 12 Math Question Paper 2079 solutions:

















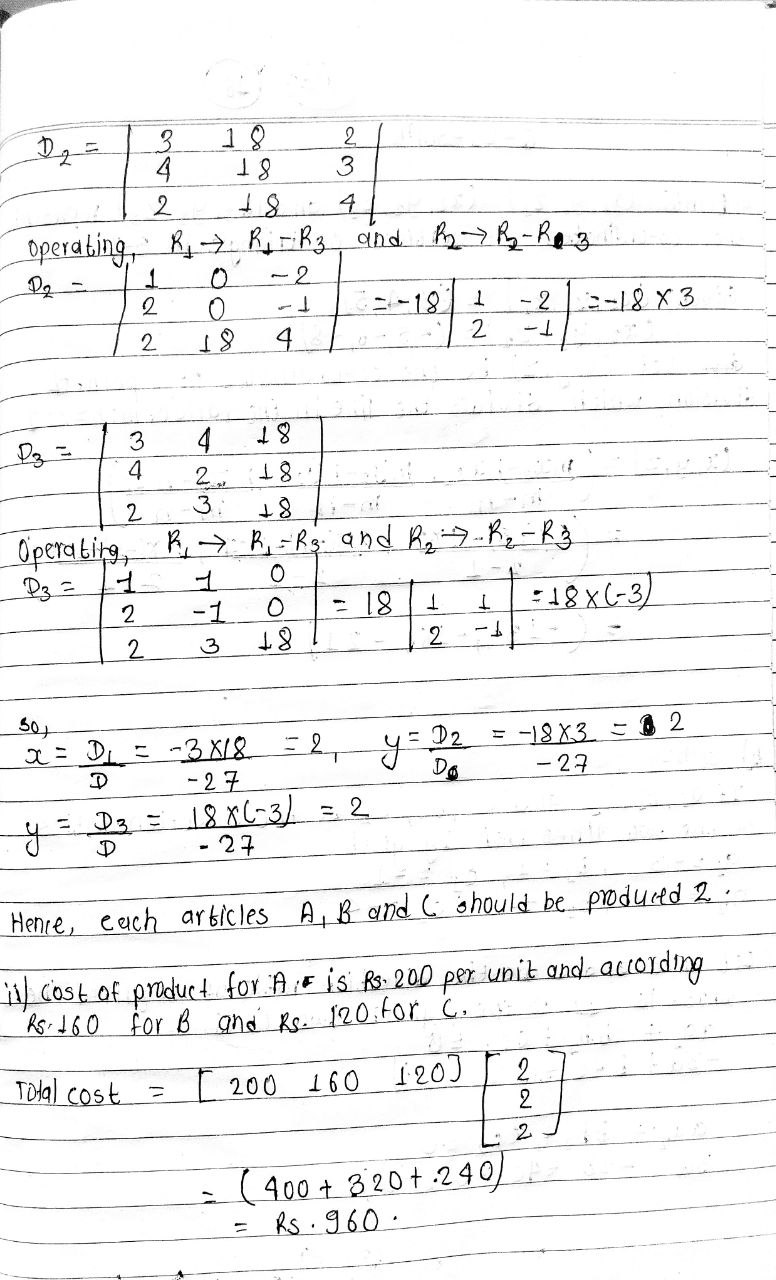






READ MORE:
Class 12 Physics Most Important Question for Neb Exam
Class 12: 91 Most Important Question of Physics
Chemistry Class 12 Most Important question for NEB Exam
Youtube Video Solution of Above Question Answer by Being Social
Source:
beingsocialnepal.blogspot.com
www.anupamsuwar.com.np


















![NEB Class 12 Exam Routine 2081/2082 [2025]](https://iswori.com.np/wp-content/uploads/2025/02/neb-class-12-routine.png)
