This note is being ready, wait for some days
Unit 1: Rotational Dynamics & Oscillatory Motion [5 hours]
Moment of inertia and torque, Rotational kinetic energy, Conservation of angular momentum, Oscillation of spring, frequency, period, amplitude, phase angle and energy.
Read:
Rotational Dynamics and Oscillatory Motion Complete Notes:
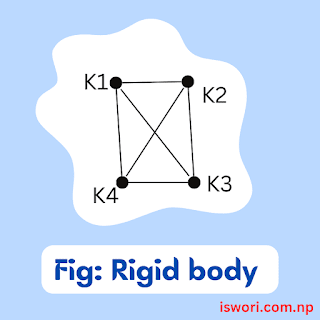
Rigid body: A body is which the distances between particles is fixed irrespective to its motion (rotational or translational) is called rigid body. In nature a perfect rigid body doesn't exist, however a solid is consider as a rigid body.
A rigid body consists of number of Constraints between particles within it.
 |
| Fig: rigid body |
K1, K2, K3, … are all constraints body.
Note:
Translation Motion:
A body with number of particles with same linear velocity is characterized by translation motion.
Rotational motion:
A body with number of particles with same angular velocity is characterized by rotational motion. A body in rotational motion has circular orbit from axis of rotation.
Moment of Inertia (M.I.)
A moment of inertia of a body in rotational motion is define as the hinderance or opposition of a body due to which its continue its own state of motion irrespective of force acting on it. It is a tensor quality. For a body, its M.I depends on the distribution or masses form axis of rotation.
For, 'F' be force acting on body in rotational motion then Torque is given by
τ = torque
τ = r F
τ = r m a [ F = m*a ]
τ = r m α r [ a = α * r ]
τ = mr^2α ----(i)
Further, torque on body is written as,
τ = I α ----(ii)
from (i) and (ii),
we get,
I = mr^2
Hence, M.I. is also defined as, the product of mass and square of its perpendicular distance form axis of rotation.
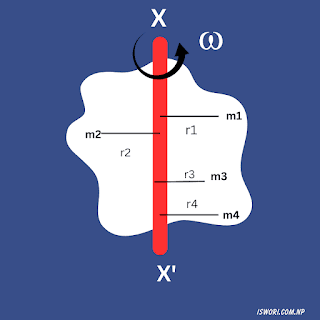
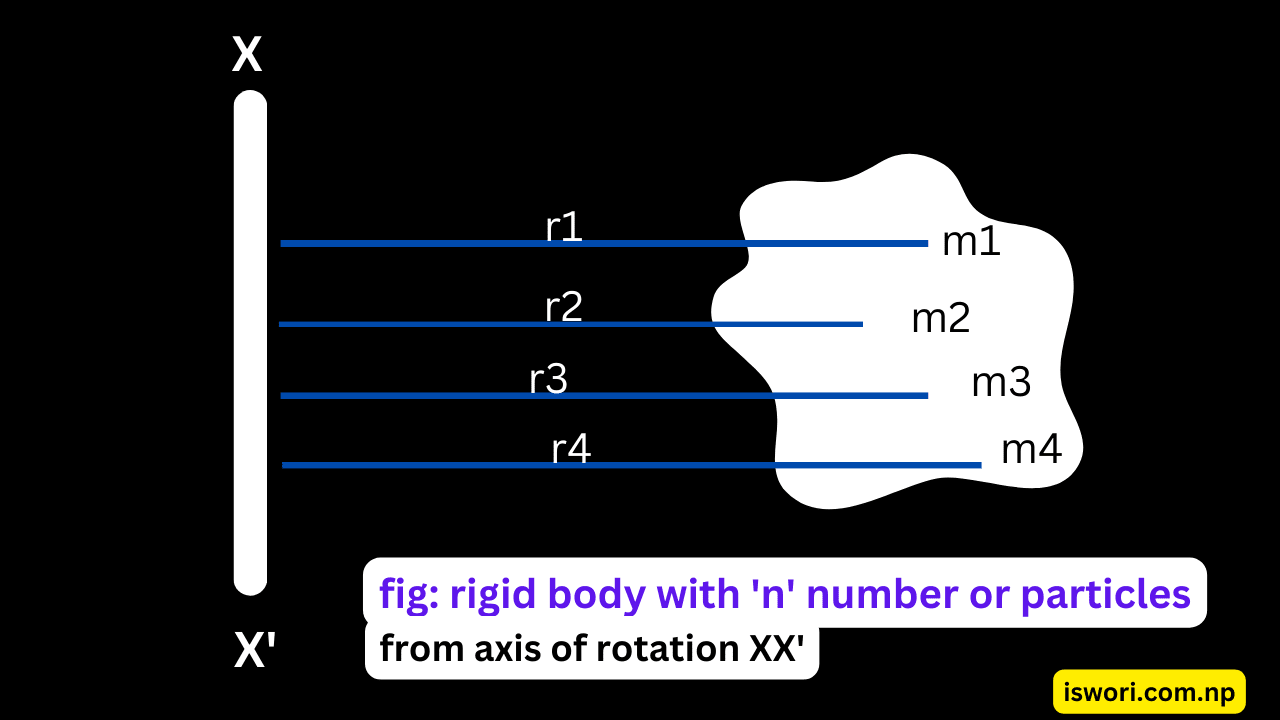
Moment of Inertia (M.I.) of having number 'n' of particles:
 |
| Moment of Inertia (M.I.) of having number 'n' of particles: |
Let us, Consider a body with 'n' number of particles with masses m1, m2, m3,....mn distributed at perpendicular distances r1, r2, r3, ...., rn form axis of rotation XX'.
then, the linear momentum at whole body about its axis of rotation XX' is
I = m1r1^2 + m2r2^2 + m3r3^2 + ….. +mnrn^2
I = i=1 to n Σ miri^2
Torque(τ) or moment of force:
A turning effect of force for a body in rotational motion is called torque. It is vector quantity. Mathematically, it is also define as the vector product of perpendicular distance form axis of rotation & the force at that point.
→ → →τ = r ⨯ F
 |
| Torque: Rotational Dynamics And Oscillatory Motion |
Direction: The direction of torque on body is perpendicular to the plane containing r & F vectors.
τ = r Fsinθ [ Where θ is angle between r & F ]
for, θ = 90° then,
τmax = r F [ Sin90° = 1 ]
Similarly, θ = 0° then
τmin = 0 [ Sin0° = 0 ]
∴ no more rotational motion.
τ = r For, τ = r m aor, τ = r m r*α [ a = r*α ]or, τ = I α [ mr^2 = I ]
Angular momentum of a rotating body [L]
The turning effect on a rotational body due to linear momentum is called angular momentum of body.
It is a vector quantity and Mathematically define as the cross product of perpendicular distance form axis of rotation with linear momentum of body. i.e.
⃯ ⃯ ⃯L = r ⨯ P
Direction of Angular momentum: The direction of angular momentum is perpendicular to plane containing r & P vectors.
L = rPsinθfor, θ = 90° then,Lmax = r P [ Sin90° = 1 ]Similarly, θ = 0° thenLmin = 0 [ Sin0° = 0 ]
L = r P
L = r m v [ P = m v ]
L = r m Ѡ r [ v = Ѡ r]
L = Ѡ m r^2
L = Ѡ I
or, L = I Ѡ
Angular momentum of a rotating body having 'n' numbers of particles:
 |
| Angular momentum of a rotating body having 'n' numbers of particles |
Let us, Consider a body with 'n' numbers of particles having masses m1, m2, m3, ….., mn at perpendicular distances r1, r2, r3, ...., rn from its axis of rotation XX'.
Further, for v1, v2, v3, …., vn be the linear velocity of 'n' particles & 'Ѡ' be the angular speed of each particles then the total angular momentum of rotating body about XX' axis is express as the sum of Angular momentum of each particle.
Conservation of Angular momentum
Principle of Conservation of Angular Momentum states that,
" In an Isolated system i.e. If an external torque is absent on it then, the total angular momentum of system is conserved. "
L = constant for τext = 0or, I Ѡ = Constantor, I ∝ 1 / Ѡ
Proof:
For a body rotating about an axis with linear momentum P at r perpendicular distance form its axis of rotation then, angular momentum of body about its axis of rotation is
Differentiate w.r.t time (t) on both sides
⃯ ⃯ ⃯L = r ⨯ PδL/δt = r ⨯ δP/δtδL/δt = r ⨯ F [ F = δP/δt , from Newton's 2nd Law of Motion ]δL/δt = τ
If τ = 0 on a system
δL/δt = 0
or dL = 0 ⇒ Initial Angular Momentum = Final Angular Momentum
On Integration,
L = Constanti.e. IѠ = Constant
For 'I1', 'Ѡ1' be M.I. & angular speed of rotating body that changed into 'I2', and 'Ѡ2' M.I. & angular speed then from conservation of angular momentum,
I1 Ѡ1 = I2 Ѡ2
Application of Conservation of Angular momentum:
A Conservation of angular momentum have huge application on our daily life, for e.g.
- Earth Rotates following conservation of angular momentum, it angular speeds increased when it is near to sum and decreased when it is far from sun.
- A ballet dancer, an ice skater or a diver can increase or decrease their angular velocity (how fast they rotate) using the principle of conservation of angular momentum.
- The falling masses of asteroids & meteoroids on planet has effect on its rotational speed due to this Principle.
Relation between Angular momentum & torque on body:
For a rigid body rotating with angular velocity 'W' & having 'I' moment of Inertia about its axis of rotation, then the angular momentum of body about that axis of rotation is given by,
L = I Ѡ
differentiate w.r to time (t)
or, dL/dt = d (IѠ) / dtor, dL/dt = I . dѠ/dtor, dL/dt = I . α --- (i) [ where α = dѠ/dt is angular acceleration ]
Further, the torque acting on a body is written as,
→ → →τ = r ⨯ Fτ = r F [ for theta = 90 degree]τ = r . dp /dtτ = r . d(mv)/dtτ = r m aτ = r m α r [ a = r α ]τ = α mr^2τ = I α --- (ii) [ mr^2 = I ]
from, eqn (i) and (ii)
τ = dL/dt
Hence, a torque on a body can also be define as rate of change of angular momentum.
i.e. If rate of change of angular momentum in a body is zero (0), then this gives that a body is under the conservation of angular momentum.
Kinetic Energy (K.E.) of rigid body in rotational motion:
Let us consider a rigid body having 'n' number of particles with masses m1, m2, m3, ….., mn distributed at r1, r2, r3, ...., rn perpendicular distance from its axis of rotation XX'.
For, 'Ѡ' be uniform angular speed of rotation of rigid body about its axis of rotation XX'. The linear velocity of each masses with vary form point to point, hence for V1, V2, V3, … , Vn be linear velocity of 'n' Particles then,
V1 = r1Ѡ, V2 = r1Ѡ, V3 = r3Ѡ, … , Vn = rnѠ
then, Rotational K.E. of body about axis XX' is given as
This is required expression for the rotational K.E. of a rigid body about its axis of rotation & this shows that rotational K.E. of body will vary with rotation of body for different axis of rotation in non-symmetrical body.
Rotational Dynamics And Oscillatory Motion: B.Sc. CSIT Physics Unit 1 Notes PDF: