SEE Math Model Question 2080 Solution (with Grid)
SEE Maths Model Question 2080 Class 10 with Solution: The Curriculum Development Centre (CDC) has released the latest academic year, 2080-2081, mathematics model question papers for all class 10 students. The model questions are available in PDF format on the CDC’s official website. The board has also provided the solution or marking scheme along with the model questions.
Check: SEE Class 10 Model Question 2080/2081
Check: SEE 2079/2080 All Province Mathematics Exam Questions
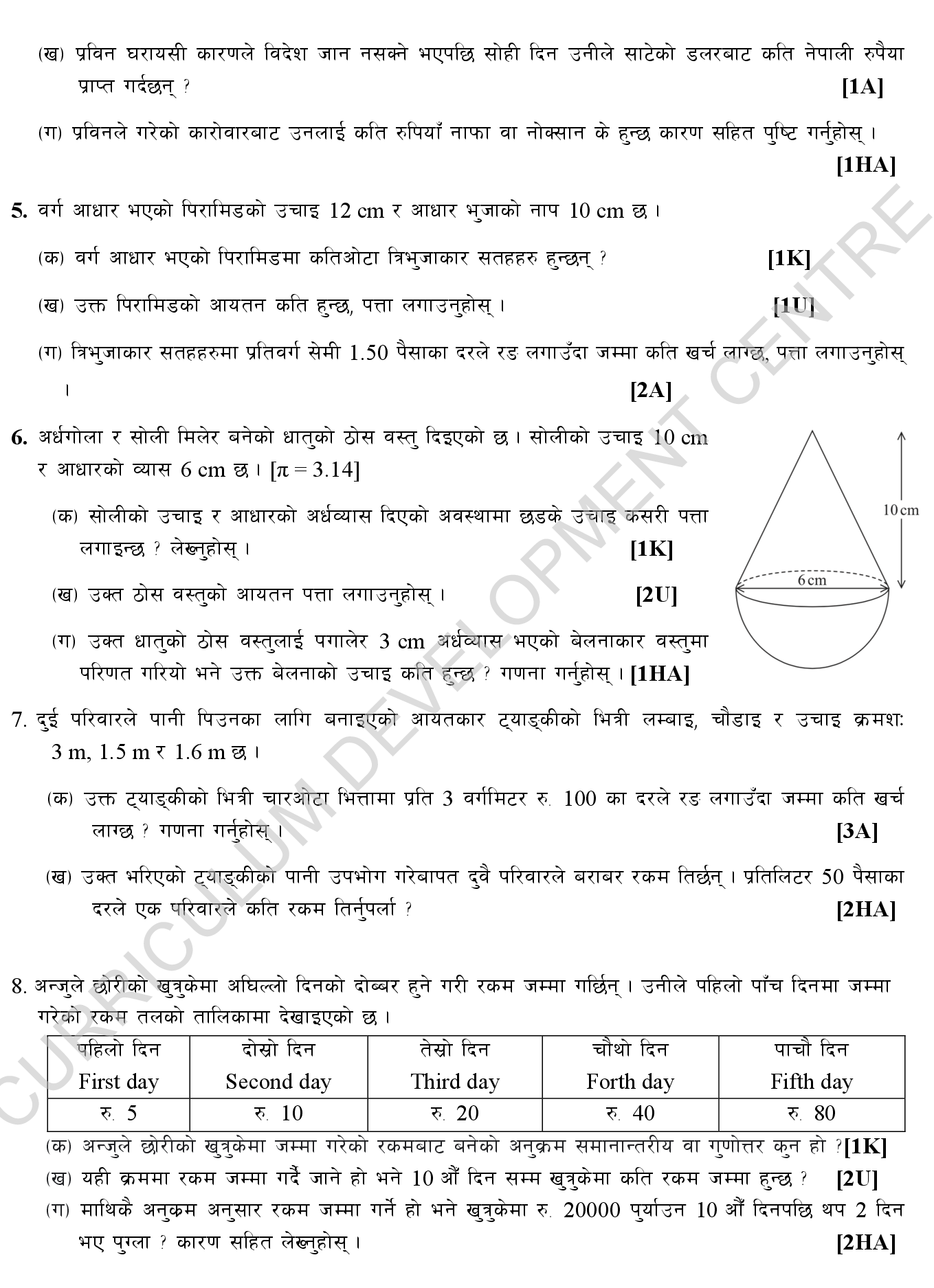
The model question paper is based on the latest CDC syllabus published for the 10th class exams 2023 at moecdc.gov.np. It gives an idea of the question paper pattern and marking scheme, and the Class 10 Mathematics Model Question Solution provide guide to practise and improve your grades for SEE Math Board Exam.
Table of Content:
SEE Math Model 2080 (In English) – Class 10
Curriculum Development Center (CDC) released model question for academic year 2080B.S.-2081B.S (2023A.D./2024 A.D.).
Complete Answer Solution of these Math model Set is provided with video solution at End of this post.
1. In a survey conducted on students studying in grade 10 at Shree
Sharada Secondary School to determine suitable place for educational trips among Pokhara,
Lumbini and Ilam, it was found that 40 students considered Pokhara to be suitable, 30 students
considered Lumbini to be suitable, and 45 students considered Ilam to be suitable. While 15
students of that grade said that all three places are suitable, 5 students did not express any
opinion.
a. If P, L and I denote the
set of students who prefer Pokhara, Lumbini and Ilam respectively, write the cardinality
notation of students for whom all places are suitable. [1K]
b. Show the above information in a Venn diagram. [1U]
c. How
many students are studying in grade 10 in the Sarada Secondary School? Calculate it. [3A]
d. If 5 students,
who did not express their opinion in the survey had said Lumbini as a suitable place, then what
would have been the ratio of students who considered only Pokhara was the suitable place and
only Lumbini was the suitable place? [1HA]
2. Bipin wants to deposit Rs 1,00,000 in a bank for 2 years. The bank offers
10% per annum compound interest with three alternates (annual compound interest, half-yearly
compound interest and quarterly compound interest)
a. Which
option among the three alternatives helps Bipin get more interest? Write it. [1K]
b. How
much amount does he receive after 2 years from compound interest compounded
semiannually? [2U]
c. At the end
of 1 year, if Bipin withdraws the total amount received according to the semi-annual
compound interest and deposits it for the rest of the period to get quarterly compound interest,
how much amount will he get at the end? [2A]
3. Sajan has Rs 1,00,00,000. Sajan purchased a car for Rs. 30,00,000 and
land for Rs. 70,00,000. For 2 years, the price of the car has been decreasing at a compound rate
of 5% per annum, while the price of land has been increasing at a certain compound rate.
a. Write the formula to find compound depreciation. [1K]
b. What will be the price of car after 2
years? Find it. [1U]
c. After 2 years, if the total price of land and car is Rs
1,05,72,700 then what is the rate of compound growth in the price of land? Calculate it.
[2HA]
4. Pravin went to the bank to exchange
US dollars in order to go abroad. According to the currency exchange rate on that day, the
buying rate of 1 US dollar was Rs.131.05 and the selling rate was Rs. 131.65.
a. How many dollars
will he get in exchange of Rs 1,57,980 Nepali rupees ? [2A]
b. How many Nepali rupees will he get back from the exchanged dollars on the
same day incase if he cannot go abroad due to family issue? [1A]
c. How much profit or loss will he get from this transaction? Write with reason. [1HA]
5. The height of the square
based pyramid is 12 cm and the length of base is 10 cm.
a. How many triangular faces
are there in square base pyramid? [1K]
b. Find the volume of the pyramid. [1U]
c. Find the cost of coloring in the triangular parts of the pyramid when the cost of
per square cm is 50 paisa. [2A]
6. A metallic solid consists of a cone and a
hemisphere. The height of the cone is 10 cm and the diameter of the base
is 6 cm. [π = 3.14]
![6. A metallic solid consists of a cone and a hemisphere. The height of the cone is 10 cm and the diameter of the base is 6 cm. [π = 3.14] Class 10 Math Model 2080 - 6. A metallic solid consists of a cone and a hemisphere. The height of the cone is 10 cm and the diameter of the base is 6 cm. [π = 3.14]](https://blogger.googleusercontent.com/img/a/AVvXsEgqc3bSq5vqWCLj9Wsb2yrF0X7FyDi3l3BA4IeAJvReddVKZX0zsi_eWBKIX7xt4z1L17JF28ar2qHNDHes_awoMEsZ5U7j7-MNXruhUq8T97phdA8Opl1r6n2zPtOUMcrydo53apHE_YCTPaAHgaVDJzyruCYNDt8E431IUDTZuUgD3A53PHEjWhZO8OhT=s16000)
a. How do you find the slanted height of the cone
when vertical height and radius of the base is given? Write it.
[1K]
b. Find the volume of the solid. [2U]
c. If the solid object was melted and turned into a
cylindrical object of radius 3 cm, what is the height of the cylinder? Calculate it. [1HA]
7. The inner length, breadth and height of a rectangular tank made for
drinking water by two families are 3 m, 1.5m and 1.6m respectively
a. What is the total cost of coloring the inner four walls of the tank at the
rate of Rs. 100 per 3 square meters? Calculate it. [3A]
b. If 2 families pay equal amounts for consuming water
from a full tank, how much will one family have to pay at the rate of Rs 50 per liter? [2HA]
8. Anju deposits money to her daughter’s piggy bank
(Khutruke) as double of previous day. The table shows the amount of money she has
deposited in first five days.
| First day | Second day | Third day | Fourth day | Fifth day |
|---|---|---|---|---|
| Rs 5 | Rs 10 | Rs 20 | Rs 40 | Rs 80 |
a. Is the
sequence made by the amount Anju deposited in her daughter’s piggy bank (Khutruke)
arithmetic or geometric? [1K]
b. If the
money is deposited in the same fashion, how much money will be deposited by the10th
day? [2U]
c. Based on the above sequence, Is 2 days enough after10 days
of deposit to collect a total of Rs. 20000? Write it with reason. [2HA]
9. The length of a
rectangular field is twice the width and its area is 72 square meter.
a. Write the standard form of the quadratic equation.
[1K]
b. Find the length and breadth of that rectangular
field. [3A]
c. How
many pieces of land can be made with dimension (6×3) square metre in that rectangular
field? Calculate it. [1A]
10.
a. Solve:
`{25}^x – 6x*5^x + 5 = 0` [3A]
b. Simplify:
`frac{m + b}{m – b} + frac{m – b}{m + b} = frac{m^2 + b^2}{m^2 – b^2}`[2U]
11. In the
adjoining figure, triangle LMZ, parallelograms
XYZM and NLZM are standing on the same base
MZ and between the same parallel lines MZ and
XL.
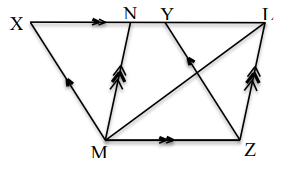
a. Write the relationship between the parallelogram
XYZM and the parallelogram NLZM. [1K]
b. Prove that the area of DMLZ is half of the area of parallelogram NLZM. [2U]
c. In the
adjoining figure, AB//CE and AC//DE. If D is the
midpoint of the AB, then prove that area of DDBC
is equal to the area of DCDE. [2HA]
![In the adjoining figure, AB//CE and AC//DE. If D is the midpoint of the AB, then prove that area of DDBC is equal to the area of DCDE. [2HA] Class 10 Math Model 2080 - In the adjoining figure, AB//CE and AC//DE. If D is the midpoint of the AB, then prove that area of DDBC is equal to the area of DCDE. [2HA]](https://blogger.googleusercontent.com/img/a/AVvXsEifX_X4BVCu7wFZ99z8YrlrsFIb-XdSpYg5TL9j-xmeuzWNv4M8-iRmXiv45JRUWrf5xoClynQA6F24sMN9GHBwerXh1JltJZc-uQJY9AIzh8uoZ6coSjmdGwaj_O0PIduXxMlP_b5iZfeGRBdyFE_9E4bRF_l75kp-BjGrMHNdkNObOokATTsceCEBu8a9=s16000)
12. O is the center of a circle. Central angle ÐLOP, inscribed angles ÐLMP and
ÐLNP are standing on the same arc LP.
a. Write the relationship between the
inscribed angles ÐLMP and ÐLNP. [1K]
b. The
measure of central angle is (9x+2)º and the measure of inscribed angle is (4x+5)º. Find the
value of x. [1U]
c. Experimentally verify the relationship between
the inscribed angles ÐLMP and ÐLNP. (At least two circles with radii 3cm are necessary.)
[2A]
13.
a.Construct a ∆PQR having sides
PQ = 7 cm, QR = 5 cm and ∠PQR = 120º
. Construct another ∆SQR whose area is equal to
the area of the given triangle. [3A]
b. In the
given figure, BC = CD and AE//BD, what is the
relationship between the ∆ABC and ∆BDE? Write
with reason. [1HA]
14. As shown in the figure,
the angle of depression of 45° when a monkey at a
height AB = 10.45m looks at a boy of height
CD = 1.45m.

a. What is the angle of elevation from the
boy to the monkey’s point of view? [1K]
b. How much high is the
monkey’s point of view than the height of the
boy? [1U]
c. Find the
distance between the tree and the boy. [1A]
d. When the monkey looks at the boy, how
many meters down or up does the monkey move from its current position to make the
angle of depression 30°?
15. The marks obtained by 40 students of Janata Secondary School in Mathematics are
given in the table below.
| Marks | No. of Students |
|---|---|
| 0 – 10 | 4 |
| 10 – 20 | 6 |
| 20 – 30 | 8 |
| 30 – 40 | 5 |
| 40 – 50 | 7 |
| 50 – 60 | 10 |
a. What does i
represent for, in the formula for finding the median (Md) = `L + frac{frac{N}{2} – cldotp f}{f}*i`. [1K]
b. Find the median from the given data. [2U]
c. Find the average score from the given
data. [2A]
d. What should be the number of students in the class with 50-60 in order to
make 30 as the average score of students? Calculate and write it. [1HA]
16. Two cards are drawn randomly one after another without replacement from a
well shuffled deck of 52 cards.
a. If
two events A and B are independent events, what is the formula for finding P(A∩B).
Write it. [1K]
b. Find the probability of
getting both are faced card. [1U]
c. Show the probability of all the possible outcomes of getting or not-getting face card in a
tree diagram. [2A]
d. If two cards are drawn randomly one after another
with replacement, how many times more is the probability that both are faced cards than
the probability that both cards are ace? [1HA]
Check: SEE 2079/2080 All Province Mathematics Exam Questions
SEE Math Model 2080 (In Nepali) – Class 10
Class 10 SEE Mathematics Model Question 2080 (in Nepali) by CDC is given as:



%20-%20Class%2010-5.jpeg)
SEE Math Model 2080 (Nepali + English) + Class 10 Math Specification Grid
New Specification grid of Class 10 Mathematics with Model Question 2080 PDF (English + Nepali) is given as:

SEE Math Model 2080 Solution (Video)
SEE Class 10 Mathematics New Model Question 2080 Solution is given as:

