Class 11 Physics Model Question
CDC Provided Updated NEB Class 11th Physics Subject Model Question 2080 Solution PDF for Upcoming Board Exam 2081. This new Class 11 Model Question is based on Latest NEB Syllabus.
| Class 11 Physics Model Question Solution 2080 | |
|---|---|
| Grade | Class 11 (XI) |
| Question Type | Model Question |
| Year | 2080-2081 |
| Total Marks | 75 Marks |
| Total Time | 3 Hours |
| Source | National Education Board |
| Provided by | Class 11 Model (All Subject) Iswori Education |



Class 11 Physics Model Question Answer Solution
Group ‘A’
1. A metre rule is used to measure the length of a piece of string in a certain experiment. It is found to be 20 cm long to the nearest millimeter. How should this result be recorded in a table of results?
(a) 0.2000 m (b) 0.200 m (c) 0.20 m (d) 0.2 m
Explanation:
From the question, it is obvious that the least count of the metre scale is 1 mm as it measures upto the millimeter. Since, 1 mm = 0.001 m . So, result should have three significant figures. Thus, [begin{align*} 20 cm &= frac{20}{100}\ therefore 20 cm &=0.200 hspace{0.01cm} m\ end{align*}]
2. Forces are applied to a rigid body. The forces all act in the same plane. In which diagram is the body in equilibrium?
(b)
Explanation:
In this case, the downward force has balanced the upward force and hence the body is in equilibrium.
3. An athlete makes a long jump and follows a projectile motion. Air resistance is negligible. Which of the following statements is true bout the athlete?
(b) The athlete has a constant horizontal velocity and constant downward acceleration.
Explanation:
In case of projectile motion, there is no horizontal force acting on the athlete(i.e., body in projectile motion) due to which there is no change in horizontal velocity. But the force of gravity is always acting towards the center of the earth with constant acceleration due to gravity always downward.
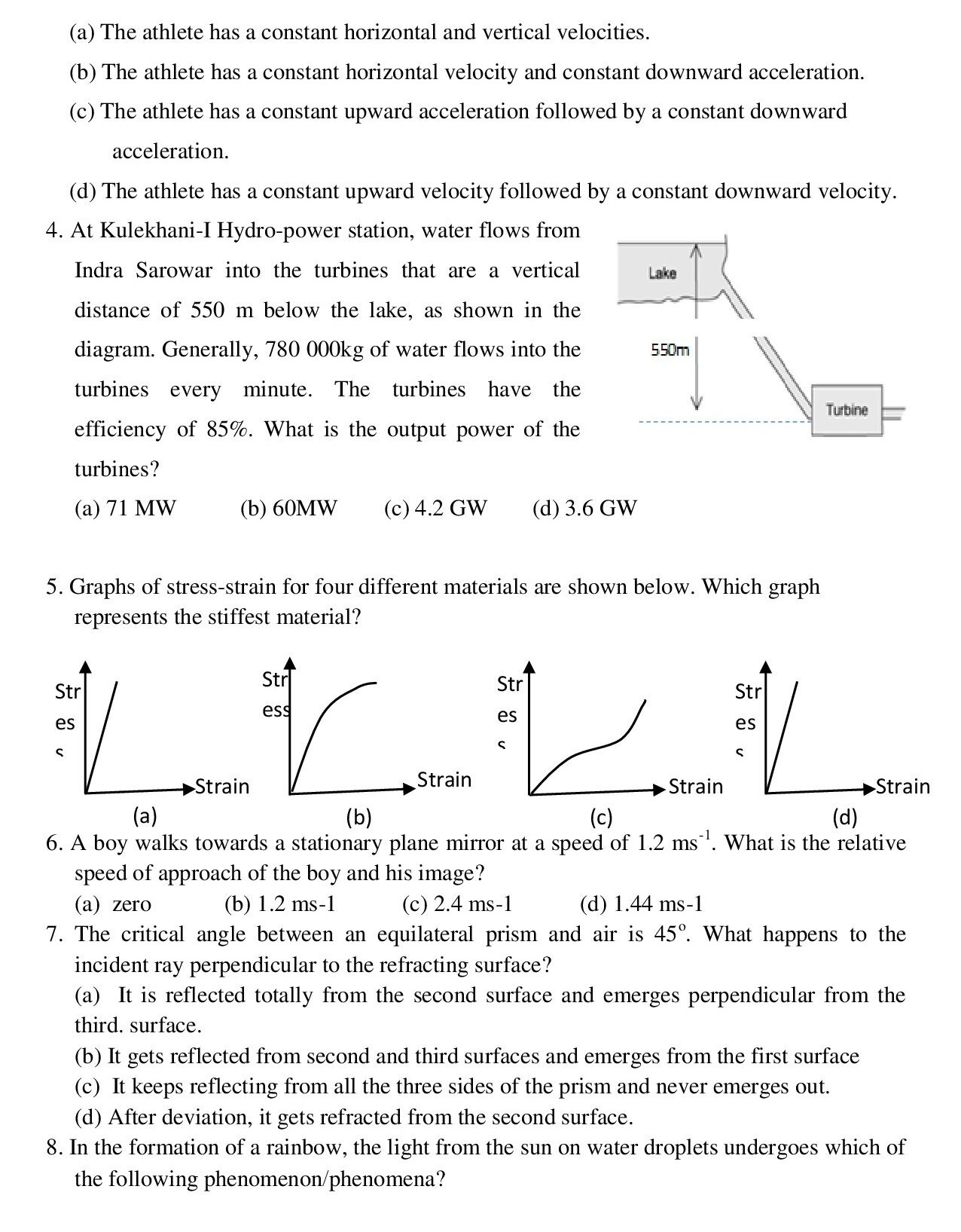
4. At Kulekhani-I Hydro-power station, water flows from Indra Sarowar into the turbines that are a vertical distance of 550 m below the lake, as shown in the diagram. Generally, 780 000 kg of water flows into the turbines every minute. The turbines have the efficiency of 85%. What is the output power of the turbines?
(b)60 MW
Explanation:
Input power (P in ) is calculated as, [begin{align*} P_{in}&=frac{mgh}{t}\ &=frac{780000times 10 times 550}{60}\ &=7.15 times 10^{7}hspace{0.1cm}W\ end{align*}] Since efficiency of machine is 85%, we can calculate Pout as, [begin{align*} P_{out}&=85%hspace{0.1cm} text{of} hspace{0.1cm} P_{in}\ &=frac{85}{100}times 7.15 times 10^7\ &=60775000\ &approx 60times 10^6 \ therefore P_{out}=60 hspace{0.1cm} MW\ end{align*}]
5. Graphs of stress-strain for four different materials are shown below. Which graph represents the stiffest material?
(a)
Explanation:
Stiffness means resistance to deformation. In graph, to find the stiffest material, we have to look for the one for which the change in strain is very small and is linear with change in stress.
6. A boy walks towards a stationary plane mirror at a speed of 1.2 ms-1. What is the relative speed of approach of the boy and his image?
(a) Zero
Explanation:
When a boy walks towards a stationary plane mirror with a speed of u(1.2 m/s), his image also travels with the same speed but in opposite direction v(= – 1.2 m/s) (i.e., towards the boy). Since, the velocity of object and image are in opposite direction, the relative velocity is, [begin{align*} V_r&=u-v\ &=1.2-(-1.2)\ therefore V_r&=2.4 hspace{0.1cm} m/s\ end{align*}]
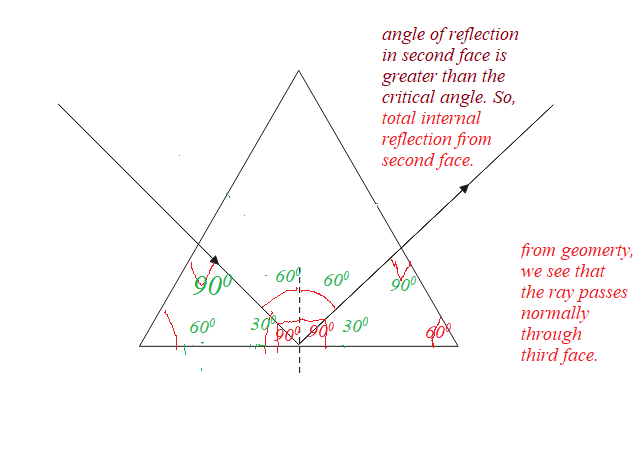
7. The critical angle between an equilateral prism and air is 450. What happens to the incident ray perpendicular to the refracting surface?
(a) It is reflected totally from the second surface and emerges perpendicular from the third surface.
Explanation:
See the figure!
8. In the formation of a rainbow, the light from the sun on water droplets undergoes which of the following phenomenon / phenomena?
c) dispersion and total internal reflection. Infact, internal reflection is involved in formation of rainbow.
9. In what unit is the power of lens measured?
(c) dioptre
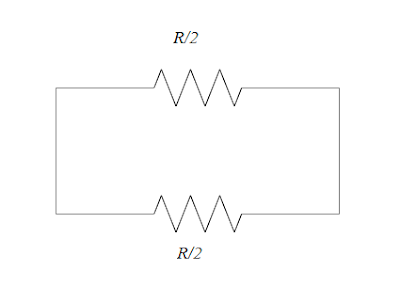
10. A piece of wire of resistance R is bent through 1800 at mid-point and the two halves are twisted together. What is the resistance of the wire thus formed?
(a) R/4
Explanation:
Since, [R propto l] When the wire is bent to two halves through 1800 and twisted together, the equal resistances (frac{R}{2}) is seen to be connected in parallel as in figure.
For parallel combination, the effective resistance is, [begin{align*} frac{1}{R_{eff}}&=frac{1}{frac{R}{2}}+frac{1}{frac{R}{2}}\ &=frac{4}{R}\ therefore R_{eff}&=frac{R}{4}\ end{align*}]
11. What are the elementary particles with half spin called?
(c) fermions
Group ‘B’
1. (a) State the law of conservation of momentum.
Solution:
It states that, ” If no external force act on the system of two colliding objects then the vector sum of the linear momentum of each body remains constant and is not affected by their mutual interaction.”
If two bodies of masses (m_1) and (m_2) are moving with respective intial velocities of (u_1) and (u_2) before collision. After some time, they collide and their final velocities becomes (v_1) and (v_2) respectively. Then from conservation of linear momentum, we write, [m_1 u_1 + m_2u_2=m_1v_1+m_2v_2]
(b) A jumbo jet of mass 4×105 kg travelling at a speed of 5000 m/s lands on the airport. It takes 2 minutes to come to rest. Calculate the average force applied by the ground on the aeroplane.
Solution:
Given,
mass, m = 4×105
speed, v = 5000 m/s
time, t = 2 min = 120 sec
average force on aeroplane, Favg = ?
[begin{align*} F_{avg}&=frac{text{change in momentum}}{text{time}}\ &=frac{mv-mu}{t}\ &=-frac{mu}{t}because v=0\ &=-frac{4 times 10^5 times 5000}{120}\ &=-1.67 times 10^7 hspace{0.1cm} N\ end{align*}] Hence, the average force exerted by the ground on the aeroplane is -1.67×107 N .
(c) After landing the aeroplane’s momentum becomes zero. Explain how the law of conservation holds here.
Solution:
Aeroplane and ground (i.e., Earth) is an isolated system of colliding objects. We know from the conservation of linear momentum that for an isolated system, the momentum before collision is equal to the momentum after collision. When aeroplane and the ground collides, the aeroplane imparts its momentum to the ground as total momentum has to be conserved. Due to this, the ground (i.e., Earth) gains the recoil velocity which is however very negligible due to the massive size of earth.
(a) State Hooke’s law.
Solution:
Hooke’s law states that the restoring force acting on a body is directly proportional to extension produced within elastic limit.
i.e., [F propto x] [-F=kx] Here, x is the extension produced on a body and k is the force constant or spring constant.
Hooke’s law can also be stated as, “For the small deformation, the stress produced on a body is proportional to the corresponding strain.” i.e., [begin{align*} text{stress} &propto text{strain}\ text{stress}& = E times text{strain} \ E&=frac{text{stress}}{text{strain}} end{align*}] Here, E is the constant of proportionality which is called modulus of elasticity of the material. Its value depends up on the material and on the type of deformation involved.
(b) The walls of the tyres on a car are made of a rubber compound. The variation with stress of the strain of a specimen of this rubber compound is shown in Fig. 1.2. As the car moves, the walls of the tyres end and straighten continuously. Use Fig. 1.2 to explain why the walls of the tyres become warm.
Solution:
The curve shown in the figure shows the phenomena ‘elastic hysteresis‘. The area between the two curves gives the thermal energy loss. When stress is applied on rubber (i.e., the wall of tyre), the energy is stored in it and some of the energy is lost in the form of heat energy as shown in figure. Thus, the walls of the tyre becomes warm.
2. (a) What is meant by specific latent heat of vaporization of water = 2.26MJkg−1?
Solution:
It means that to vaporize 1 kg of water, 2.26 MJ of heat energy is to be supplied on it.
(b) A 1.0 kW kettle contains 500g of boiling water. Calculate the time needed to evaporate all the water in the kettle. (Specific latent heat of vaporization of water = 2.26MJkg−1).
Solution:
power of a heater, P = 1 kW = 1000 W
mass of boiling water, m = 500 g = 0.5 kg
specific latent heat of vaporization of water, L = 2.26 MJ/kg = 2.26×106 J/kg
time needed to evaporate all the water, t = ?
Now, the heat required to boil the water is,
[begin{align*} Q&=mL\ &=0.5 times 2.26 times 10^6\ therefore Q&=1.13 times 10^6 hspace{0.1cm} J\ end{align*}] Again,
[begin{align*} P&=frac{Q}{t}\ t&=frac{Q}{P}\ &=frac{1.13 times 10^6}{10^3}\ &=1.13 times 10^3\ therefore t&=1130 hspace{0.1cm} s\ end{align*}]
(c) Explain why the actual time needed is a little longer than the time calculated in 2(b).
Solution:
Since the efficiency of any real machine is always less than 100%, the kettle does not deliver the power of 1 kW and thus the time taken is longer than the calculated.
3. (a) State any three properties of an ideal gas as assumed by the kinetic theory of gas.
Solution:
The three properties of an ideal gas as assumed by the kinetic theory of gas are,
(i) The gas molecules are in random motion.
(ii) There exists no intermolecular force of attraction between the gas molecules.
(iii) The collision between the gas molecules or between the gas molecules and the container is elastic in nature.
(b) A student needed to use the ideal gas for a certain experiment. But, the ideal gas does not exist. Suggest what two different things this student could do to solve his problem.
Solution:
At low pressure and high temperature, the volume of the real gas is negligible and the kinetic energy of the molecules is quite large as compared to the mutual force between them. Hence, he could lower the pressure and increase the temperature to approximate the ideal gas and use in his experiment.
4. (a) Define temperature gradient in an object.
Solution:
The rate of change of temperature of an object with respect to the distance in the direction of the maximum change of temperature. [text{Temperature gradient}=frac{dtheta}{dx}] Here, (dtheta) is the difference in temperature and (dx) is the distance along the maximum change in temperature.
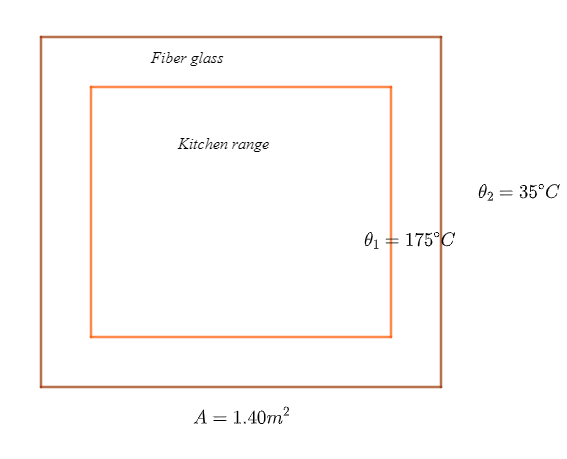
(b) An electric kitchen range has a total wall area of 1.40 m2 and is insulted with a layer of fiber glass 4 cm thik that has a inside temperature of 175oC and its outside surface is 35 oC. The fiber glass has a thermal conductivity of 0.040 Wm-1K-1. Calculate the rate of flow of heat through the insulation, assuming the fibre as a flat slab of area of 1.40 m2.
Solution:
area of fiber glass, A = 1.40 m2
thickness of fiber glass, x = 4 cm = 0.04 m
higher temperature, θ1 = 1750 C
lower temperature, θ2 = 350 C
thermal conductivity of fiber glass, k = 0.040 Wm-1K-1
rate of heat flow, Q/t = ?
Now,
[begin{align*} frac{Q}{t}&=frac{kA(theta_2-theta_1)}{x}\ &=frac{0.040 times 1.40 times (175-35)}{0.04}\ therefore frac{Q}{t} &= 196 hspace{0.01cm} W\ end{align*}] Hence the rate of heat flow is 196 W .
(c) How might the rate of conduction be affected if the fiber absorbs moisture? Justify your answer.
Solution:
Thermal conductivity of the fiber will increase with increase in the moisture content as it increases the rate of heat transfer by conduction.
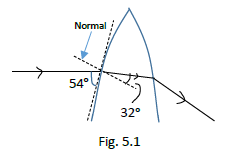
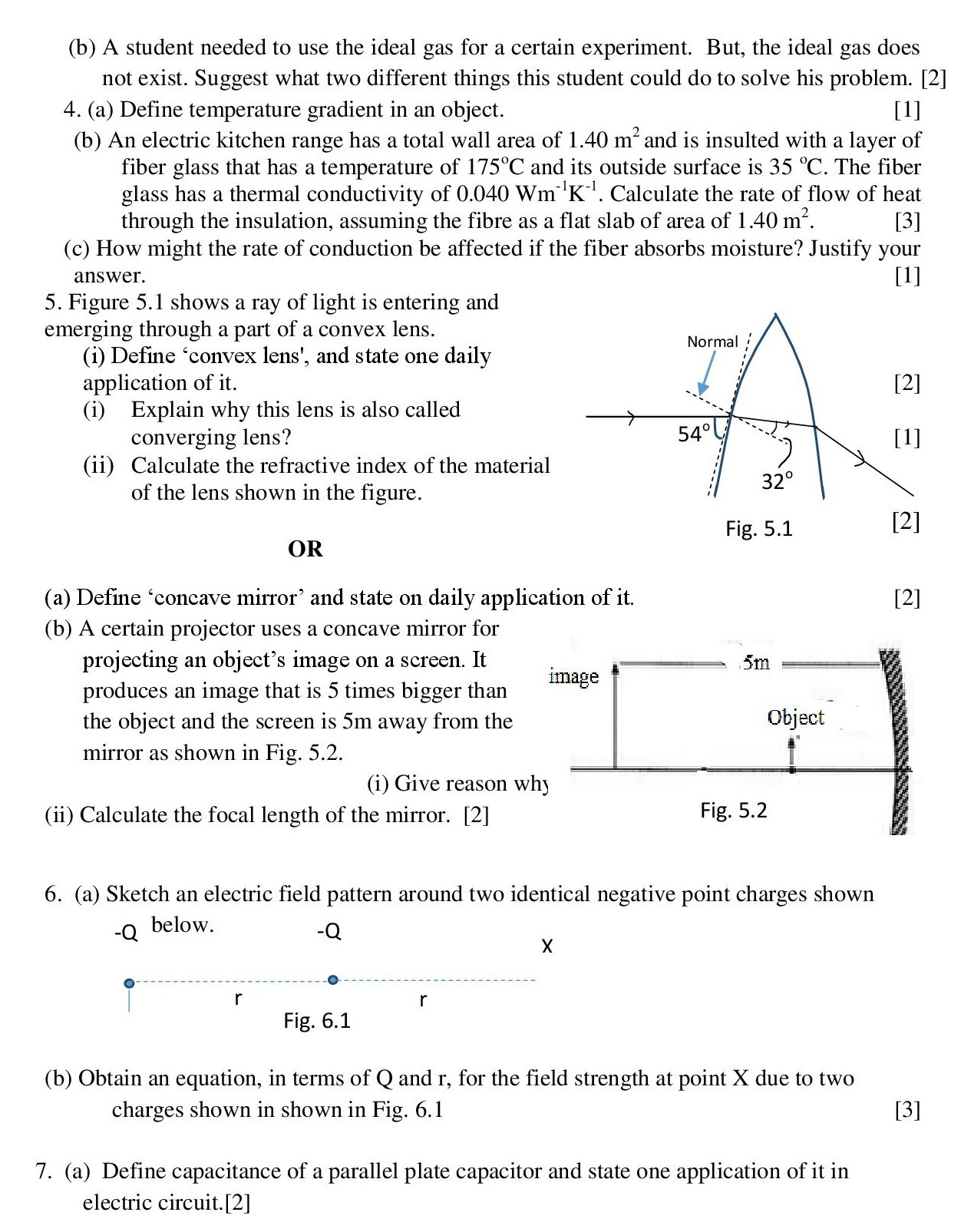
5. Figure 5.1 shows a ray of light is entering and emerging through a part of a convex lens.
(i) Define ‘convex lens’, and state one daily application of it.
Solution: A lens which is thick at the centre and thin at the edges is called a convex lens. It is also called the converging lens. Convex lens is mainly used in magnifying glasses and to put one, we can say that it is used to treat hypermetropia.
(ii) Explain why this lens is also called converging lens?
Solution: Converging of rays means to meet the rays at a fixed point. Convex lens converges the parallel rays to a fixed point on its principal axis (i.e., at Focus). It is shown in figure.
(iii) Calculate the refractive index of the material of the lens shown in the figure.
Solution:
angle of incidence, i = 900-540 = 36 0
angle of refraction, r = 320
refractive index, μ = ?
Now,
From Snell’s law,
[begin{align*} mu&=frac{sini}{sinr}\ &=frac{sin 36^circ}{sin 32^circ}\ therefore mu&=1.11 \ end{align*}] Hence the refractive index of the material is 1.1.
(a) Define ‘concave mirror’ and state one daily application of it.
Solution: Concave mirror is a spherical mirror whose reflecting surface is caved in. Concave mirror is used in shaving mirror as it produces a larger image of a face that is upright as well as in nature.
I guess there is some typo or printing mistake in question no.(b) because of which I have not solved it here. I have explained my side in video. Please watch that for explanation. (Click here!)
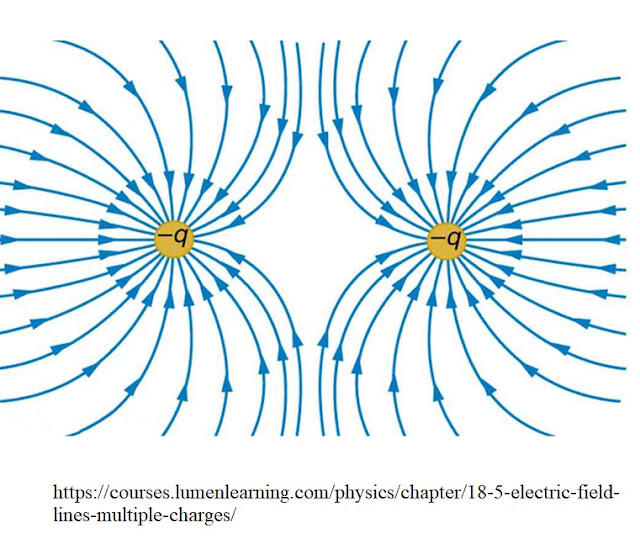
6. (a) Sketch an electric field pattern around two identical negative point charges shown below.
Solution:
(b) Obtain an equation, in terms of Q and r, for the field strength at point X due to two charges shown in shown in Fig. 6.1
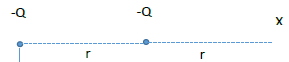 |
| Fig 6.1 |
Solution:
The electric field strength is, [E=frac{Q}{4pi epsilon_0 r^2}] So, at point X, we can find the electric field due to the charges as, [begin{align*} E&=-frac{Q}{4pi epsilon_0 (2r)^2}+left(-frac{Q}{4pi epsilon_0 r^2}right)\ &=-frac{Q}{4pi epsilon_0}left(frac{1}{4}+1right)r^2\ therefore E&=-frac{5Q}{16pi epsilon_0 r^2}\ end{align*}]
7. (a) Define capacitance of a parallel plate capacitor and state one application of it in electric circuit.
Solution:
Capacitance of a parallel plate capacitor is the ability of a parallel plate capacitor to store charge which is mathematically written as, [C=frac{epsilon_0 A}{d}] Where, C is the capacitance, ε0 is the permittivity of free space, A is the area of the plate of capacitor and d is the distance between two plates of capacitor.
Capacitor is used in rectifiers to filter the a.c. out of mixed d.c. components.
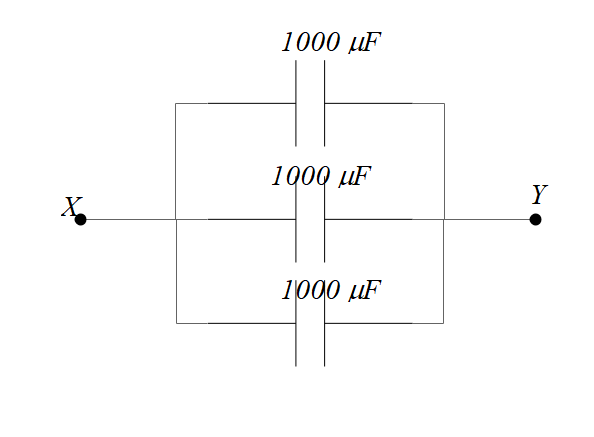
(b) Three capacitors each of 1000μF are connected in an electric circuit as shown below.
Solution:
The combination is parallel
The effective capacitance of parallel combination of capacitors is equal to the sum of their capacitances.
[C=1000+1000+1000=3000hspace{0.1cm} mu F]
8. (a) What is meant by a power of a heater is 2kW?
Solution:
It means that 2000 J of electrical energy is converted into the thermal energy by the heater.
(b) Calculate the resistance of the above mentioned heater when it is connected to 220V source.
Solution:
power, P = 2000 J
voltage, V = 220 V
resistance, R = ?
Now,
[begin{align*} R&=frac{V^2}{P}\ &=frac{220^2}{2000}\ therefore R&=24.2 hspace{0.1cm} Omega\ end{align*}] Hence, the resistance of the heater is 24.2 Ω.
(c) Suggest what changes must be done to the heater so that it gives more heat. Justify your answer.
Solution:
From the Joule’s law of heating, [H=I^2Rt] For constant R, heat depends on (I^2) and t. So, by increasing the current (with rheostat adjusted) and flowing the current through the heater wire for longer time t.
Group ‘C’
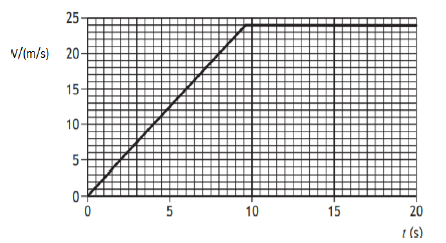
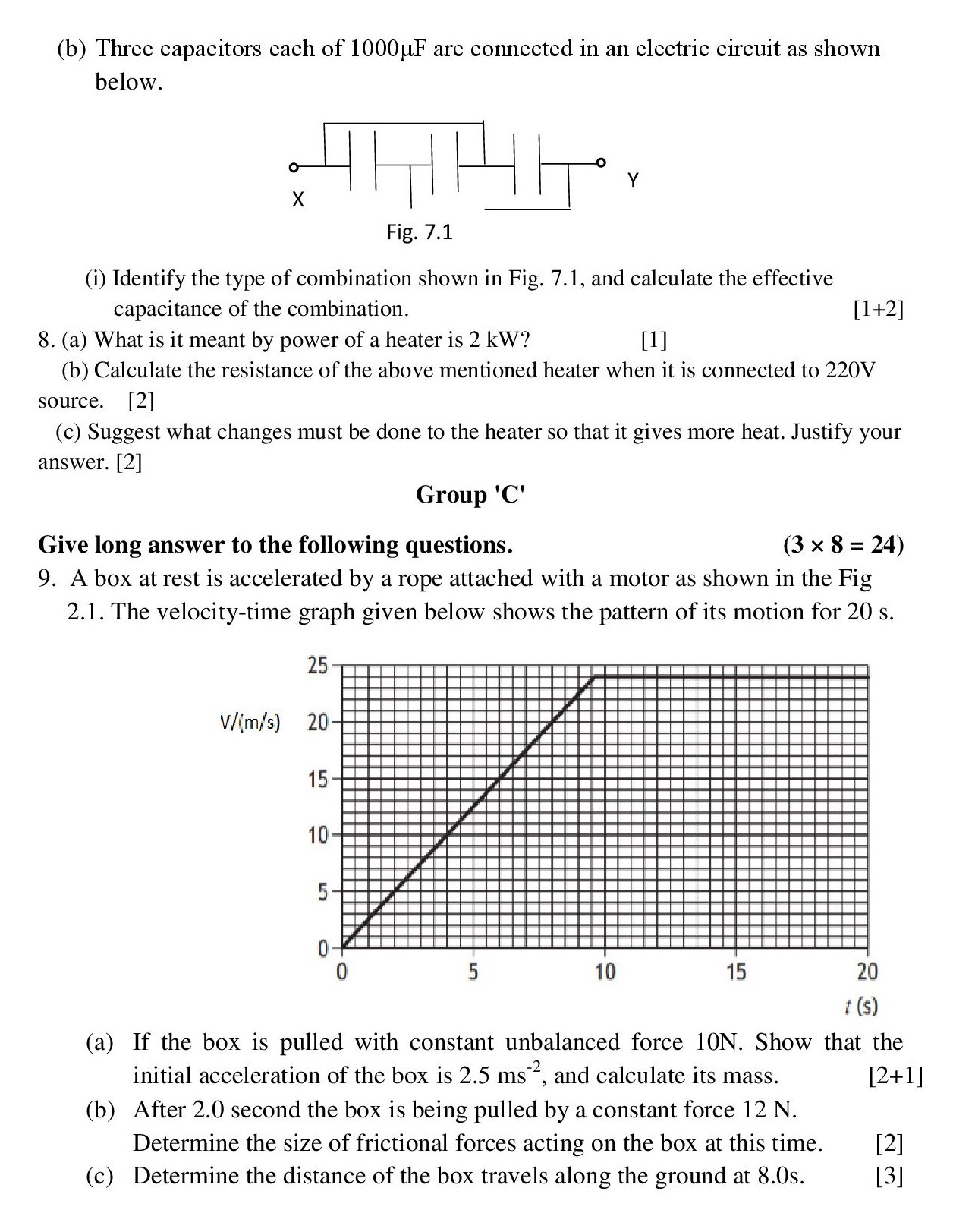
9. (a) A box at rest is accelerated by a rope attached with a motor as shown in the Fig. The velocity-time graph given below shows the pattern of its motion for 20 s.
(a) If the box is pulled with constant unbalanced force 10 N. Show that the initial acceleration of the box is 2.5 m/s2, and calculate its mass.
Solution:
Acceleration is the rate of change of velocity. Taking time from 0 to 5 sec ( See x-axis ), we see the change in velocity as 12.5 m/s. [begin{align*} a&=frac{Delta v}{Delta t}\ &=frac{12.5}{5}\ therefore a&=2.5 hspace{0.1cm} m/s^2\ end{align*}] From Newtons second law of motion,
[begin{align*} F&=ma\ m&=frac{F}{a}\ &=frac{10}{2.5}\ therefore m&=4 hspace{0.1cm} kg\ end{align*}]
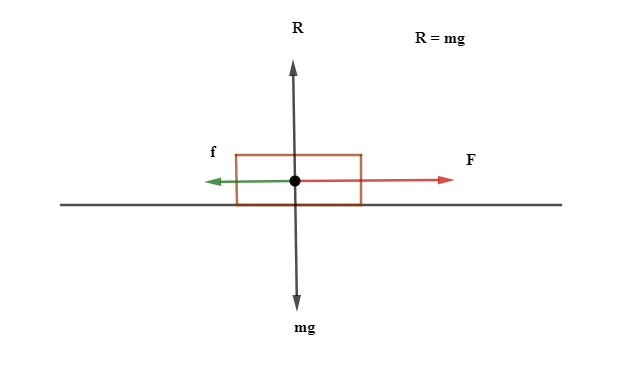
(b) After 2.0 second the box is being pulled by a constant force 12 N. Determine the size of frictional forces acting on the box at this time.
Solution:
Since the sliding body experiences frictional force in the opposite direction (see the diagram below), the net force is,
[begin{align*} F-f&=ma\ 12-f&=4 times 2.5\ 12-f&=10\ therefore f&=2 hspace{0.1cm}N\ end{align*}]
(c) Determine the distance of the box travels along the ground at 8.0s.
Solution:
When calculating distance, we find the area of the curve or line upto which we have to calculate the distance.
Upto 8 sec, [t=8] [Delta v=20] Thus, the distance is calculated as,
[begin{align*} &=frac{1}{2}times t times Delta v\ &=frac{1}{2} times 8 times 20\ &=80 hspace{0.1cm} m\ end{align*}]
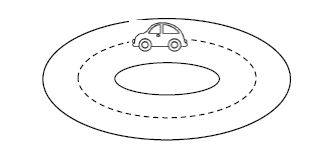
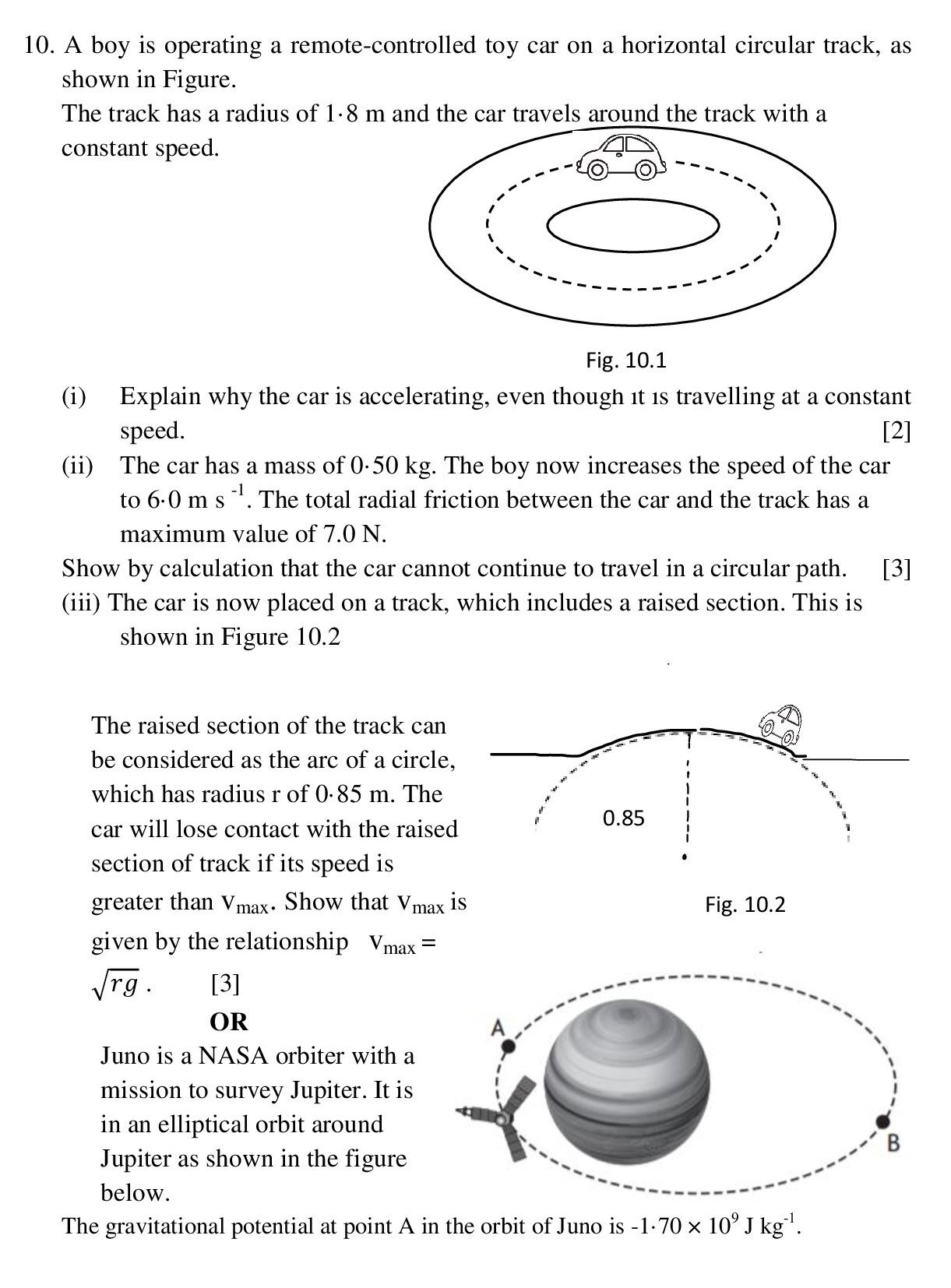
10. A boy is operating a remote controlled toy car on a horizontal circular track, as shown in Figure.
The track has a radius of 1·8 m and the car travels around the track with a constant speed.
(i) Explain why the car is accelerating, even though it is travelling at a constant speed.
Solution: During circular motion, the velocity of the body changes continuously (since their direction changes). As acceleration is the change in velocity, it also changes.
(ii) The car has a mass of 0·50 kg. The boy now increases the speed of the car to 6·0 m/s. The total radial friction between the car and the track has a maximum value of 7.0 N. Show by calculation that the car cannot continue to travel in a circular path.
Solution:
The necessary centripetal force for the toy car to move in a a uniform circular motion is provided by the friction between the car and the track. So, for the car to move in a track, the frictional force should be equal to the centripetal force required to move the car in circular motion. Calculating the necessary centripetal force as, [begin{align*} F_c&=frac{mv^2}{r}\ &=frac{0.50 times 6^2}{1.8}\ therefore F_c&=10 hspace{0.1cm} N\ end{align*}] Since, the force of friction between the car and the track i.e., 7 N is less than the necessary centripetal force i.e., 10 N, the car cannot continue to travel in a circular path.
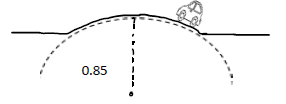
(iii) The car is now placed on a track, which includes a raised section. This is shown in Figure.
The raised section of the track can be considered as the arc of a circle, which has radius r of 0·85 m. The car will lose contact with the raised section of track if its speed is greater than vmax. Show that vmax is given by the relationship vmax = √𝑟𝑔 .
Solution:
We know the normal force acting on the car is, [N=frac{mv^2}{r} – mg] at the top point.
For maximum velocity, [begin{align*} frac{mv_{max}^2}{r}&=mg\ therefore v_{max}=sqrt{rg}\ end{align*}]
Juno is a NASA orbiter with a mission to survey Jupiter. It is in an elliptical orbit around Jupiter as shown in the figure below.
The gravitational potential at point A in the orbit of Juno is -1·70 × 109 J kg-1.
(a) State what is meant by a gravitational potential at point A is -1·70 × 109 J kg-1.
Solution: It means that 1.70×109 J of work is done on unit mass of a body to bring it from infinity to the point A without acceleration.
(b) At point B, Juno is 1·69 × 108 m from the centre of Jupiter. If the mass if Jupiter is 1.90 ×1027 kg, calculate the gravitational potential at point B.
Solution:
Gravitational potential at point B is calculated as,
[begin{align*} V_B&=-frac{GM}{r}\ &=-frac{6.67 times 10^{-11} times 1.90 times 10^{27}}{1.69 times 10^8}\ &=-7.5 times 10^8 hspace{0.1cm} J/kg\ end{align*}]
(c) The mass of Juno is 1·6 × 103 kg. Determine the change in gravitational potential energy if Juno moves from Point A to Point B.
Solution:
The gravitational potential energy is, [U=-frac{GMm}{r}=-Vtimes m] Thus the change in gravitational potential energy from point A to point B is calculated as, [begin{align*} U_A-U_B&=-V_Atimes m-(-V_B) times m\ &=m(V_B=V_A)\ &=1.6 times 10^3 times (-7.5 times 10^8 + 1.70 times 10^9)\ therefore U_A-U_B&=-1.5 times 10^{12} hspace{0.1cm} J\ end{align*}]
11. (a) Explain how Rutherford’s α-scattering experiment suggested that the nucleus of an atom is very small, very dense and positively charged.
Solution:
In his alpha scattering experiment, Rutherford directed the energetic alpha particles at a thin gold foil and measured the extent to which they are deflected as they passed through the foil. The respective suggestions of alpha scattering experiment are:
- (i) Small nucleus: Most of the alpha particles were either undeflected or only slightly deflected but a few are deflected through large angles. It suggests that, the nucleus is very small as the influence is seen only for small fraction of alpha particles.
- (ii) Very dense and positively charged nucleus: Some of the alpha particles were deflected backward which means that there should exist large force inside the atom. This large force could only be provided if the positive charge (because alpha particle is positive and thus for it to be deflected requires another positive charge), instead of being spread throughout the atom, were concentrated tightly at its center. It suggests that the nucleus is very dense and positively charged.
(b) Considering that the α-particles carry average kinetic energy of 2.00 x 1010 J, calculate the maximum size of the gold nucleus. [Atomic number of gold is 79 and e= 1.60 x 10-19C]
Solution:
Guys! I want you to know that the typical energy range of alpha particle is 3 to 7 MeV which is 4.8×10-13 J to 1.12×10-12 J. In the question, the kinetic energy of the alpha particle is 2.00×1010 J which is a printing error. So, I will use the kinetic energy of alpha particle as 5 MeV i.e., 8×10-13 J. Did you find how I changed MevV to J? Don’t be confused! Just use the relation [1MeV=1.6times 10^{-13} J]
Given,
Kinetic energy of the alpha particle, Kα = 5 MeV = 8×10-13 J
charge of alpha particle, q1 = +2e
charge of gold nucleus, q2 = +79e
Now,
The kinetic energy of the alpha particle is transferred to the electric potential energy as the alpha particle enters the atom. The transfer is complete when the alpha particle momentarily stops at the distance d of the closest approach to the taget nucleus (i.e., gold nucleus). Thus, [begin{align*} K_{alpha}&=U\ &=frac{1}{4pi epsilon_0}frac{q_1 q_2}{d}\ d&=frac{q_1 q_2}{4 pi epsilon_0 K_{alpha}}\ &=frac{2times 79 times (1.6times10^{-19})^2}{4 pi times 8.854times 10^{-12}times 8times 10^{-13}}\ therefore d&=4.54times 10^{-14}hspace{0.1cm} m\ end{align*}] Though not completely correct, the maximum size of the gold nucleus, i.e., its diameter can be written as, [2d=9.08 times 10^{-14} hspace{0.1cm} m]
(c) Explain why the radius of the gold nucleus must be much smaller than the value calculated in 11(b) above.
Solution:
To be more precise, the value calculated above i.e., d is actually the distance of the closest approach between nucleus and the alpha particle. This in no way can represent the size or radius of the gold nucleus. Even if the alpha particle had touched the gold nucleus, it would be wrong to interpret 2d as the actual size of nucleus.
Also Check: Class 11 Model Question (All Subject)
Class 11th Physics PDF Download
Also Check
Class 11 Model Question (All Subject)
Class 12 Model Question (All Subject)