Volumetric Analysis Numericals Problems - Class 12 Chemistry

Volumetric Analysis Numericals Problem Solution

Grade 12 Chemistry Chapter 1 Volumetric Analysis Numericals Questions Answer Solution

 

Normality

Normality is defined as the no. of gram equivalent of solute present in one liter of the solution. It is represented as N.

`\text{Normality}\text{ = }\frac{\text{No}~\text{of}~\text{gm}~\text{eq}~\text{of}~\text{Solute}}{\text{V}~\text{of}~\text{Solution}~\left(\text{in}~\text{L}\right)}`

No. of gm eq. = V of Solution (in L) * Normality

`No. of gm eq. = \frac{V*N}{1000}`

`\text{Normality}\text{ = }\frac{\text{Wt of solute in gm}}{\text{Eq wt * V of Solution (in L)}}`

`\frac{\text{Wt}~\text{of}~\text{solute}~\text{in}~\text{gm}}{\text{Eq}~\text{wt}\text{ * }\frac{\text{V}~\text{of}~\text{Solution}~\left(\text{in}~\text{mL}\right)}{\text{1000}}}`

`\text{Wt. of Solute in gm}\text{ =}`

`\frac{\text{Normality}\text{ * }\text{Eq}~\text{wt}\text{ * }\text{V}~\text{of}~\text{Solute}~\left(\text{in}~\text{ml}\right)}{\text{1000}}`

`\therefore w = \frac{VEN}{1000}`

The solution obtained by dissolving one gram equivalent weight of solute in one

liter of solution is called normal solution.

`No\ of\ gm\ eq = \frac{Wt\ of\ Substance\ ( gm)}{Eq \ Wt}`

Similarly, the solution obtained by dissolving 1/10th gram equivalent weight of solute in one liter of solution is called decinormal solution.

Compounds	Molecular wt.	Equivalent wt.	n
Hydrochloric acid	36.5	36.5	1
Sulphuric acid	98	49	2
Oxalic acid	126	63	2
Sodium hydroxide	40	40	1
Sodium carbonate	106	53	2
Calcium carbonate	100	50	2
Aluminium	27	9	3
Magnesium	24	12	2

---

How many gram of sodium carbonate is required to prepare 250ml of decinormal solution of sodium carbonate?

Calculate the concentration of solution obtained by dissolving 0.63gm of oxalic acid into 200ml of solution.

Molarity

Molarity of a solution may be defined as the no. of moles of solute present in one liter of

the solution. It is represented as M.

The solution obtained by dissolving one gram equivalent weight of solute in one liter of solution is called normal solution.

`No\ of\ Moles = \frac{Wt\ of\ Substance\ ( gm)}{Mol. \ Wt}`

Similarly, the solution obtained by dissolving 1/10th mole of solute in one liter of solution is called decimolar solution.

Gm/liter:

The amount of solute in gram that is present in one liter or 1000ml of solution is called

gram per liter.

Relationship between normality and molarity:

Percentage (%)

The amount of solute in gram that is present in 100ml of solution is called percentage (by volume).

Some Important Formula

1) Express the following in g. eqvt. and moles

i) 1.06 g. Na 2 CO 3

We have, g. eqvt.

 = `frac{given wt}{eqvtwt} `

= `\frac{1.06}{53} = 0.02`

no. of moles

= `frac{given wt}{eqvtwt} `

= `\frac{1.06}{106} = 0.01`

ii) 150 ml. of 0.1M NaOH solution

We have, g. eqvt. = normality x vol. in litre

= `0.1*\frac{150}{1000}` (in NaOH, N =M)

= 0.015

No. of moles = molarity x vol.in litre

= `0.1*\frac{150}{1000}`

= 0.015

2) Calculate the wt. of anhydrous Na2CO3 required to prepare 250 ml. of  `\frac{N}{20}(f = 1.01)` solution.

We have, `X = \frac{NEV}{1000}`

`= \frac{1*1.01*53*250}{20*1000}`

= 0.67 g

3) How many kg of wet NaOH containing 12% water are required to make 120 L of a 0.25 N solution.

We have,`X = \frac{NEV}{1000}`

`= \frac{0.25*40*120*1000}{1000}`

= 1200 g.=1.2 kg.

Let the wt. of wet NaOH be y g.

A/Q, (100-12) % of y = x

or, `\frac{88}{100}*y`=1.2 kg.

or, y = 1.363 kg.

4) You are given a L of semi molar solution of oxalic acid. What volume of water should be added into it to make it exactly decinormal?

Here, V1 = 1L         V2 = (1+x) L

S1 = `\frac{M}{2}` = 1N

S2 = `\frac{N}{10} `= 0.1 N

(In oxalic acid, N = 2M)

We have, from normality equation:

V1 S1 = V2 S2

or, 1 * 1 = (1 + x)  * `\frac{N}{10} `

or, 1+ x =10

or, x = 9 L

 

5) Concentrated hydrochloric acid has a specific gravity of 1.16 & contains 32% HCl by wt. calculate the vol. of this acid which would be required to make 10 L of a normal solution of the acid.

a) Calculation of concentration of conc. HCl

We have, Normality   `= \frac{\% (\frac{w}{w})*sp.  gravity*10}{eqvt wt\ldotp }`

 `= \frac{32*1.16*10}{36.5}`

= 10.17 N

b) Calculation of vol.

Here, V1 =?     V 2 = 10 L

S1 = 10.17 N     S2 = 1 N

We have, from normality equation:

`V_1 S_1 = V_2 S_2`

or, V 1 x 10.17 N = 10 x 1 N

V1= 0.983 L

6) x g. of oxalic acid reacts completely with 20 ml. of `\frac{N}{10}(f = 1.06)` ` KMnO_4` solution. Calculate the value of x.

Here, g. eqvt. of oxalic acid = g. eqvt. of KMnO4

or, `(\frac{given wt.}{eq. wt})_`Oxalic acid = ( normality*g. eqvt. of `KMnO_4)`

`\frac{X}{63} = 0.1*1.06*\frac{20}{1000}`

X = 63*0.1*1.06*0.02g. 

X = 0.133g. 

7) If 20 ml. of `\frac{N}{20}(f = 2.06)` `H_2SO_4` and 30 ml.of `\frac{N}{10}(f = 1.12)` HNO 3 are mixed together, calculate the normality of mixture.

We have,  `V_m S_m = V_1 S_1 + V_2 S_2`

or, (20 +30) * `S_m` = 20 * 0.05 * 2.06 + 30 * 0.1 * 1.12

or, `S_m` x 50 = 2.06 + 3.36

or, `S_m` = 5.42/50 

∴ `S_m` = 0.1084 N

8) What volume of semi normal and centimolar `H_2SO_4` solutions should be mixed in order to prepare 1.5 L of decinormal solution of `H_2SO_4`?

Let, `V_1` = y         `V_2` = 1.5-y

`S_1 = \frac{N}{2}`

`S_2 = \frac{M}{100} = \frac{N}{50}`

We have,  `V_m S_m = V_1 S_1 + V_2 S_2`

or, `1.5 * \frac{N}{10} = y * \frac{N}{2} + (1.5-y) * \frac{N}{50}`

or, 0.15 = 0.5y + 0.03 – 0.02y

or, 0.48y = 0.12

or, y = `\frac{0.12}{0.48}` = 0.25 L

Thus, the vol. of semi normal `H_2SO_4 `= y = 0.25 L

The vol. of centimolar `H_2SO_4 ` = 1.5-y = 1.5-0.25=1.25 L

9) 30 c.c. of 0.2N HCl, 10 c.c. of 1N `H_2SO_4 `, 20 c.c. of `\frac{N}{10}`HNO3 and 40 c.c. of water are mixed together. What will be the normality of the mixture?

We have, `V_m S_m = V_1 S_1 + V_2 S_2+V_3 S_3 + V_4 S_4`

or, 100 x `S_m` = 30 x 0.2 + 10 x 1 +20 x 0.1 + 40 x 0

or, 100 x `S_m` = 6 + 10 + 2 + 0

or, `S_m` =  `\frac{18}{100}` = 0.18N

Read: Class 12 Chemistry Notes

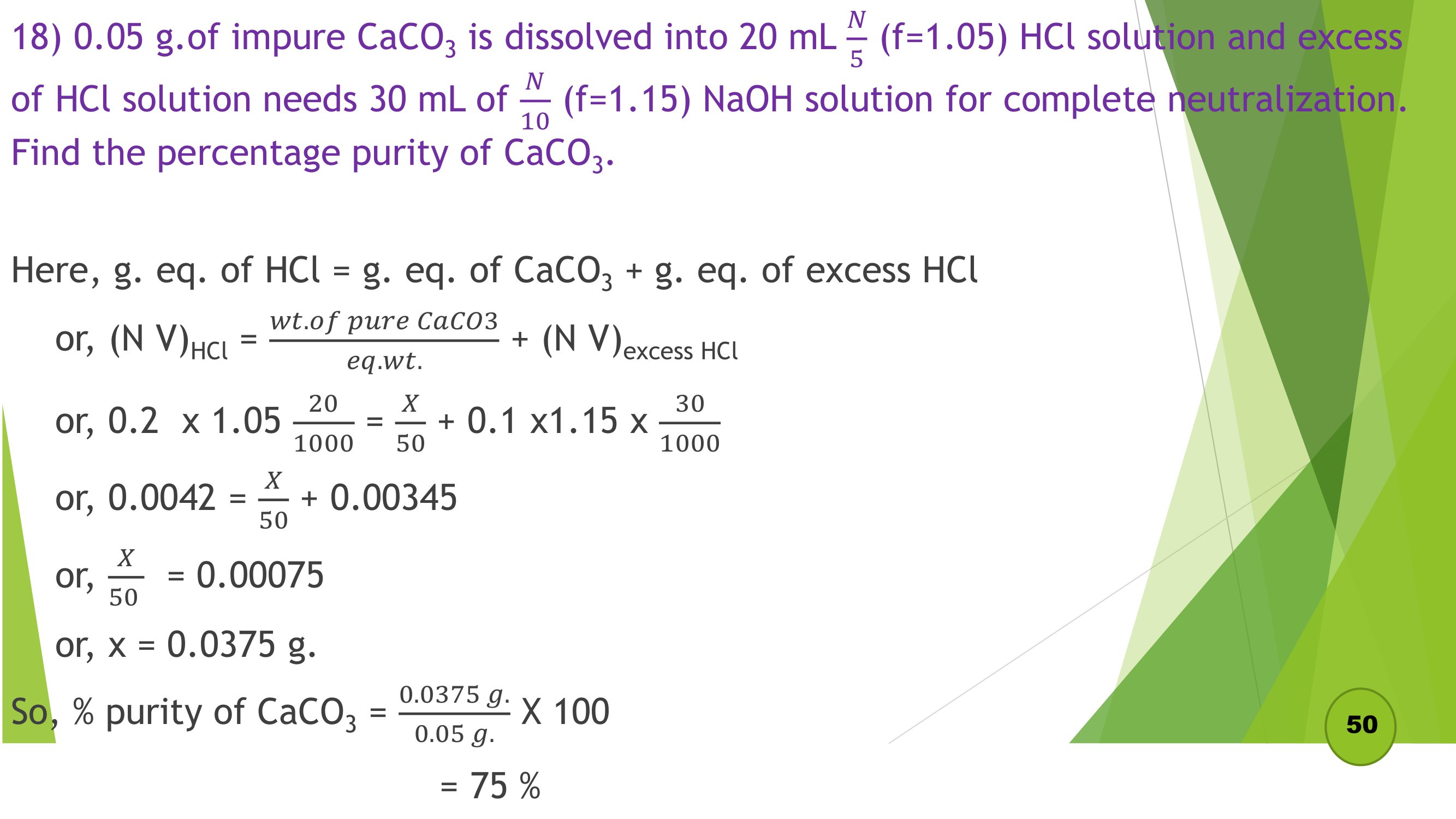
Remaining Numericals

---

Volumetric Analysis Numericals PDF

---

Read: Volumetric Analysis Note - Class 12 Chemistry